From Linked Lists to Namespace Merkle Trees
A Retrospective and Prospective on Data Structures in Blockchain Commitments
We’ve covered in relative depth how both Merkle and Verkle trees work in our article “Beyond IBC”. However, there are other applications and derivatives of Merkle trees that we do think deserve their own article, because of their unique properties.
In this article, we are referring to Namespace Merkle Trees (NMT), Merkle Tree Mountain Ranges (MMR), and also Jelly Merkle Trees (JMT). This article will thus serve to explain some interesting aspects of them, their use cases, and hopefully, you’ll want to further explore data structures further.
A History of Data Structures
Merkle trees are the most commonly mentioned data structure when talking about the inner workings of many infrastructure projects in the blockchain industry. They are named after Ralph Merkle, who patented the concept in 1979 after introducing them in his paper “A Certified Digital Signature”.
The fact they have received so much attention in the crypto industry is hardly surprising, as they have been a critical data structure in commitments to the global state and transactions roots of blockchains. The most clear-cut example of this is the fact that Merkle Trees were first mentioned on page 4 in the original bitcoin whitepaper. The stated main advantage of using Merkle Trees in the block header was to allow nodes to discard spent transactions, consequently saving disk space.
As part of scalability research (including statelessness), a lot of resources have been put into altering Merkle Trees. This is because as we try to scale blockchains in a way that does allow people to keep running nodes (why? See end user verification) resource usage must be minimized. Through that lens, the various ‘flavours’ of Merkle Trees are fascinating innovations for scaling and security within blockchains and infrastructure projects.
One thing that does warrant being said, before we dive into the various data structures we’d like to showcase, is that some of them have different purposes. For example, JMTs, Patricia’s (in ETH) and Verkle trees are used to commit to the global state root, while NMTs and MMRs are used in transaction Merkle roots. However, both’s roots (top node) would commonly be provided in a block header. In Ethereum’s case, standard Merkle trees are used for transaction data, while a Patricia tree is used for the global state tree.
Namespace Merkle Trees
Namespace Merkle Trees, also known as "NMTs," are a type of data structure that is used to organize and verify large collections of data on a blockchain. As a variant of the aforementioned and more well-known Merkle Tree data structure, they offer a number of advantages in terms of efficiency and scalability when it comes to applications and rollups requesting data specific to them. They were initially presented in the LazyLedger paper presented by Mustafa Al-Bassam of Celestia in 2019 as part of his PhD.
One of the key benefits of NMTs is their ability to organize data into a hierarchical structure, wherein you can efficiently verify individual or separate pieces of data that an application requests. As a user, you only need to retrieve the corresponding leaf node and its parent nodes, rather than the entire dataset.
Another advantage is its ability to scale to very large collections of data. This is made possible by the use of multiple levels of "namespace" nodes, which allows for hierarchical organization.
As with any Merkle tree structure, they use cryptographic hash functions to combine (hash) the data in each node, which ensures that the data cannot be modified without detection. Additionally, their hierarchical structure allows for efficient and secure verification of the integrity of said data.
Every chain (“rollup”) on top of Celestia has its own namespace, for which the data is merkelized and sorted. The final result is one short Merkle root, where each rollup has its own subtree (namespace) that it can pull and watch data from. This is especially relevant for blockchains with potentially more blockspace per block (while enabling light clients to be first-class citizens through DAS) as it allows you to pull data without having to pull the entire block.
As such, an NMT on Celestia is a Merkle tree with the nodes ordered by namespace IDs and the hash function modified so that every node in the tree includes the range of namespaces of all its child nodes. If an application or rollup requests data for a specific namespace, the DA layer (Celestia) then supplies datasets for the specific data relevant to that application as a result of its unique namespace ID and provided nodes in the tree. This allows us to check that the provided data has been made available in Celestia blocks, hence the name Data Availability (DA).
Another implementation of NMTs is the ones used by Sovereign Labs, a ZK sovereign rollup, who have been implementing them in Rust.
Merkle Tree Mountain Ranges (MMR)
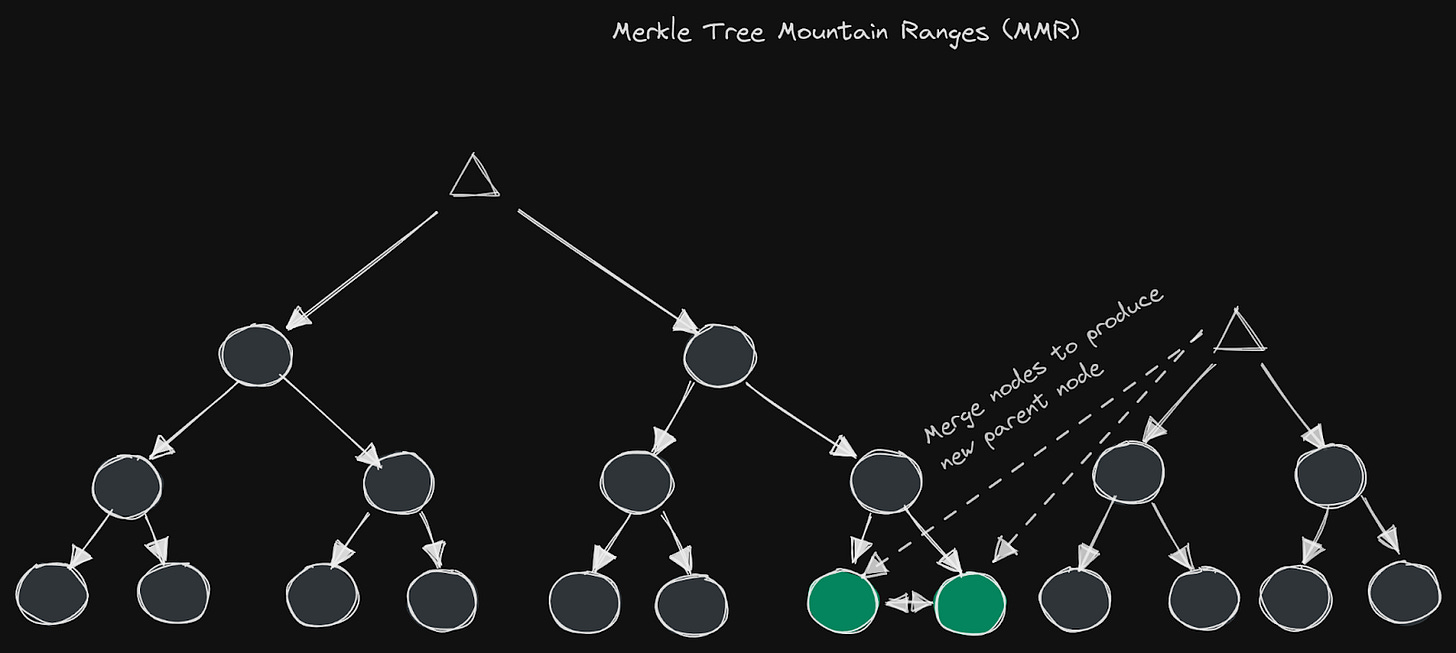
A Merkle Tree Mountain Range (MMR) is a data structure that is used to maintain a consistent large log of data that is easily accessible without providing the entire tree. It is also based on the concept of a Merkle tree. In an MMR, each leaf node represents a piece of data, and the hashes at each level of the tree are computed by attaching the hashes of the child nodes and applying a hash function.
The MMR structure allows for particular efficient insertion of new data and the ability to prove the existence of an existing distinct piece of data within the tree. The name “Mountain Range” refers to the specific construction of the tree; It is constructed in such a way that it always tries to maintain the largest possible consistent single binary tree (binary meaning that each node has at most two child nodes), which can result in the tree structure having multiple “peaks” (hence the mountain) or sister trees. When the root nodes of an MMR are needed, the peaks of the individual trees must be batched together to compute the root hash of the entire MMR (the block header, root (top) node of a Merkle tree for example). This makes MMRs a useful tool for maintaining a consistent and long-term secure and verifiable record of data, where certain parts can be updated and referenced as needed.
Now imagine this on a larger scale, and you get the concept of MMRs.
The ability to efficiently prove the existence of a particular piece of data within an MMR makes it useful for non-interactive state proofs, alongside Verkle Trees, which we’ll cover further down. A state proof is a method of verifying the current state of a system without requiring direct interaction with that system. In the context of an MMR and Verkle Tree, a state proof might be used to verify the current state of the data within the tree without having to directly access the tree itself.
This means you can allow a prover to provide a compact proof of the inclusion of a particular piece of data within the MMR. The proof can then be verified by a verifier using the root hash (known as block header in block commitments) of the MMR and the hashes (child nodes) at the appropriate levels of the tree for the data needed. By utilizing this method, it allows the verifier to confirm the authenticity of the proof without having to access the data in the MMR directly. Appending an element to an MMR is much more efficient, as you don’t need to navigate through the entire tree to include a new dataset. All of this can be achieved on-chain, which allows for full transparency. However, MMRs are much more expensive in terms of gas than Merkle tree proofs to verify on-chain (Comparison, note append gas and verification gas being different, although committing to an MMR is cheaper). In most use cases, MMRs would become infinitely large and not able to be verified on-chain (as a result of gas usage), hence off-chain verification via an open-source “trustless” ZKP setup in many cases.
Herodotus is an example of a project utilizing MMRs for their non-interactive state proofs, wherein the data required is computed into a ZKP, which can then be verified as needed. This allows them to keep a consistent state of verifiable data that can be refreshed and accessed as needed.
Jelly Merkle Trees (JMT) and Tiered Commitment Trees (TCC)
Originally developed by the Libra/Diem team for what was supposed to become the Facebook/Meta chain, Jellyfish Merkle Trees (JMTs) are a modified version of AR16MT. JMTs have several features that set them apart from other implementations of Merkle trees. Namely, version-based node keys which allow for smaller key sizes on average, reduced complexity with less node types, and a concise proof format—meaning less space usage and faster computation. They function to provide what was called either “Proof-of-Inclusion/Exclusion”. Which tracks the binary path to the intended node.
Penumbra is another project that is utilizing JMTs, although with some changes. Penumbra uses them to record all values related to the chain such as valset, proposals, assets etc. This, despite the chain providing privacy, obviously still needs to be stored and available to clients, so that they can verify that the information is indeed correct. A sparse Merkle tree, such as JMTs is ideal for such a purpose.
On any other blockchain, full nodes handle all transactions and keep a record of the entire chain state. Clients can check the accuracy of the data with Merkle tree commitments. On Penumbra, however, the chain only stores cryptographic commitments to private user data, and lets clients handle transaction execution and instead provide ZKPs to ensure that transactions are computed correctly. The implication of this is that clients must create Merkle proofs for verification by full nodes, but as the number of users on the chain grows, the burden on clients to process every transaction becomes unsustainable. To address this issue, they use a Tiered Commitment Tree (TCT), a light SNARK-friendly Merkle tree with subtrees that enables clients to ignore transactions that do not affect them.
Note that a root refers to the “top” node (which is what is provided in a block header), while child nodes are also known as leaves(leaf)—hence a tree.
Verkle Tree Integrations
Now that we have discussed various flavours/alterations of Merkle Trees it can be interesting to look at one integration that Verkle Trees can achieve. As mentioned, Merkle Trees can bring improvements to the resource usage of nodes, this is why they were used in Bitcoin in the first place. One big effort in this area is using Verkle Trees to reach what has been coined “statelessness”. Statelessness is the concept of allowing nodes to disregard state they have no interest in (read more). One instance could be that state not updated over a year could be disregarded by a node. However, this state will remain revivable at a later time via polynomial commitments. This would vastly reduce the resource requirements for nodes. Verkle Trees are a critical component of this because they enable smaller proof sizes, which makes statelessness (either weak or full) feasible. These advantages are a result of the parent node being an offshoot of vector commitments rather than hashing functions. However, this comes at the cost of compute efficiency, as mentioned in our previous article.
Other projects utilising Verkle trees to lower the resource usage of nodes and make their data commitments to chains more efficient are Polymer and Lagrange. Lagrange is compiling Merkle trees into Verkle trees for smaller commitments, so that the eventual Zero-Knowledge Proof (ZKP) that gets posted on another chain is much smaller and less costly than initially. Furthermore, vector commitment based proofs (which Verkle trees are) can be aggregated easier in a user’s browser than Merkle proofs within zkSNARKs. For this same reason, Polymer eventually wants to move to Verkle trees, as covered in our “Beyond IBC” article. They’re both using Plonky2 as their ZKP scheme for the on-chain verification.
This is just an example of cool shit you can do with Merkle tree alterations. We hope that it either piqued your interest in data structures or has driven you to research parts of blockchain infrastructure that you might not otherwise have looked at. If you're working on anything in this domain, reach out to us!
Also many thanks to Mathijs van Esch for helping with parts of the article, and for providing the discussion leading to this.